Differentials

Previously, we talked about differentials. These refer to the differences in input and output for a simple passthrough of the S-Box. In practice, we're interested in how a differential propagates through multiple rounds of a cipher, all steps included.

To keep things simple, we'll only focus on finding distinguishers for now on. That is, ways to differentiate a cipher from random output. Later, we'll discuss how to turn distinguishers into key recoveries.

Following the differential

Let's focus on two-round PRESENT.

A normal round of PRESENT consists of a round key addition, the substitution, and then the permutation. We recall that in the last round, we only do the key addition part. This means, for 2-round PRESENT, our input is only going through an S-Box once, as seen below.

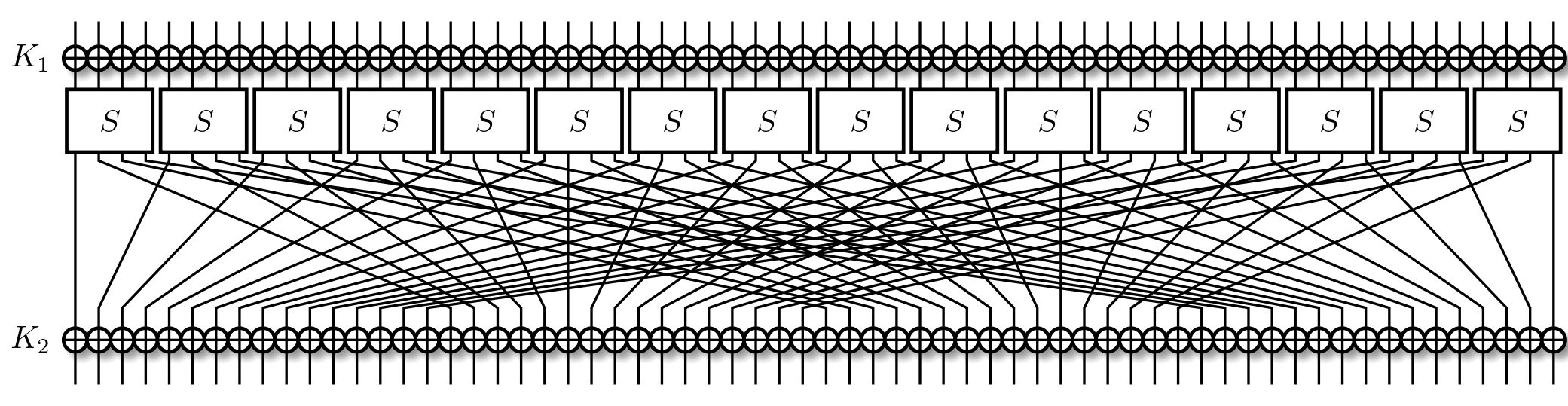
Since we care only about the differences in inputs and outputs, and the round keys are constant, we can safely ignore their impact on the differential. This should be rather clear as $$x \oplus y = (x \oplus K_a) \oplus (y \oplus K_a)$$

We've discussed the S-Box already. We have a differential and are running on the pretense that a certain difference will hold with a certain probability that we can distinguish. What remains to be seen is how this differential scatters due to the permutation layer. Let's reuse our example from earlier, and suppose we have $\Delta_{\text{in}} = 7$. To simplify our discussion, we will use $x_0, x_1,\ldots , x_{15}$ to denote the intermediate difference in each step. The values $x_0, x_1,\ldots , x_{15}$ are 16 nibble differences, with $x_0$ being the least significant nibble difference.

Let's place our input difference in the most significant nibble, i.e. let $x_{15} = \Delta_{\text{in}} = 7$.

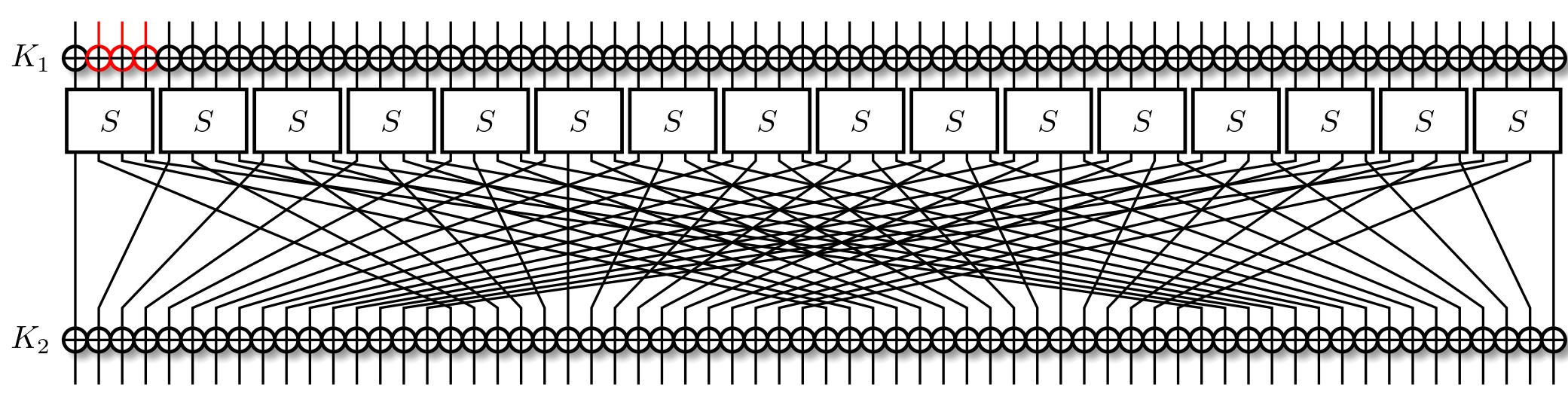
We'll reuse the differential $7 \rightarrow 1$ from the previous lesson. Post-substitution, we then have that $x_{15} = 1$. This is then permuted by the next layer, and then the second round key addition occurs. Following the permutation, we have that $x_{3} = 8$.

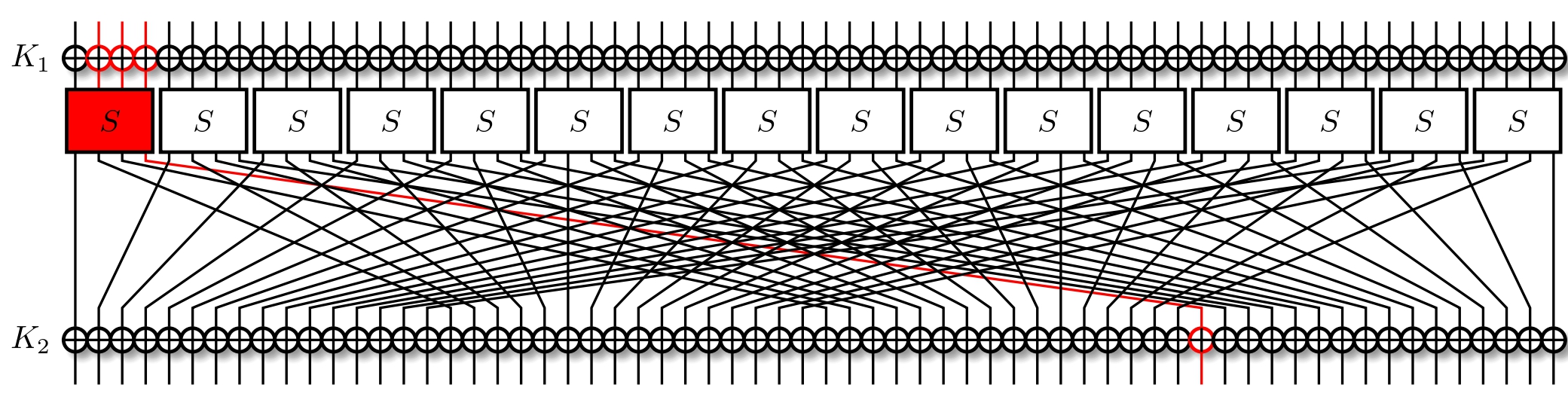
Recall that the probability that this differential holds is $p = \frac{4}{16} = 0.25$. This implies that we can expect that, for one out of every four input pairs, the corresponding output pairs will differ by exactly $x_{3} = 8$ with all else being the same. Formally, for our two rounds, we can say that $$ \text{Pr}[\text{Enc}(x\oplus \text{(0x7 $\ll$ 60)}) = \text{Enc}(x) \oplus \text{(0x8 $\ll$ 12)}] = 0.25 $$

With this, we have traced our differential. It's now natural to be curious whether we can extend it.

Distinguishing from random

Now that we have a differential, it remains to be seen how useful it really is. What does it mean for us to have a difference in the output, and how can we use this?

The procedure for exploiting a differential would be as follows:

1. Find a differential $x \rightarrow y$ that holds with a probability $p$
2. Generate a random input $r$ and encrypt $(r, r \oplus x$)
3. For an output $(c_1, c_2)$ check whether $c_1 \oplus c_2 = y$. Repeat this many times, and estimate how often it holds

If our outputs exhibit a differential property largely in line with how often we expect it too, then it's likely that we're dealing with real ciphertext. Otherwise, it could be just random data. Note that random data, assuming a 64-bit block size, can exhibit any difference with a probability of $2^{-64}$. This is what we're trying to beat with our own differentials.

Differentials that enable us to distinguish ciphertext from random data are called differential distinguishers. Later we'll see how we can push this further, and recover a key. But first, we'll look at how we can get more meaningful ones.