Differential trails

We've talked about finding a differential, and how to use one. However, we've barely attacked PRESENT thus far. For a cipher with 32 rounds, tackling just two (really, it was one and a half) seems silly. This is what we seek to address with this section.

Recall that a differential is the observed difference following an S-Box. We define a differential trail as our set of differences as we follow a differential through the cipher. Sometimes this is referred to as a differential characteristic instead. Some authors may make a distinction between the two terms. For simplicity, both mean the same thing to us.

Trails

Previously, we actually used the differential $7 \rightarrow 1$ to make a rather basic trail. Traditionally, trails are noted by making a note of the entire state as follows, arrows connecting rounds. $$\text{0x7} \ll 60 \rightarrow \text{0x8} \ll 12$$ As this isn't helpful when constructing these trails on our own, and does little to really show what the impact of the permutation layer is, we will use the following notation for the duration of the course: $$ \begin{array}{|c|c|c|c|} \hline \text{Round} & & \text{Differences} & \Pr \ \hline \text{I} & & x_{15} = 7 & 1 \ \hline \text{R1} & S & x_{15} = 1 & 2^{-2} \ \hline \text{R1} & P & x_{3} = 8 & 1 \ \hline \end{array} $$

The second column denotes the layer of the round. We ignore the key addition step for brevity as it has no impact on the difference. The last column denotes the probability of our difference holding. The total probability of a differential trail is the product of all its differentials' probabilities.

This isn't a particularly impressive trail as it spans more than one round only by technicality, but it lays the groundwork for what we want to achieve. From now on, we'll be looking at the real deal: 32-round PRESENT. It's worth noting that if we find a trail that spans, say, four normal rounds, it effectively works on a 5-round variant of PRESENT.

Continuing our trail

We left off at $x_{3} = 8$, so we need to look at what new differential to add onto our trail. For this, we consult our DDT, looking at the row for $\Delta_{\text{in}} = 8$:

  Δ  0 1 2 3 4 5 6 7 8 9 a b c d e f
------------------------------------
8 |  0 0 0 2 0 0 0 2 0 2 0 4 0 2 0 4

Recall that it's in our interest to pick differentials with high probability of occurrence. We'll go with the choice of $8 \rightarrow \text{b}$ for our next differential, once more holding with probability $0.25$. We now have that $$ \begin{array}{|c|c|c|c|} \hline \text{Round} & & \text{Differences} & \Pr \ \hline \text{I} & & x_{15} = 7 & 1 \ \hline \text{R1} & S & x_{15} = 1 & 2^{-2} \ \hline \text{R1} & P & x_{3} = 8 & 1 \ \hline \text{R2} & S & x_{3} = \text{b} & 2^{-2} \ \hline \text{R2} & P & x_{4} = 8, x_{11}=8, x_{15}=8 & 1 \ \hline \end{array} $$ Note that our differential is now seen in three bits as $\text{0xb} = \text{0b1011}$. From this, due to the permutation, we will have up to three S-Boxes active in the second round. In fact, we have exactly three.

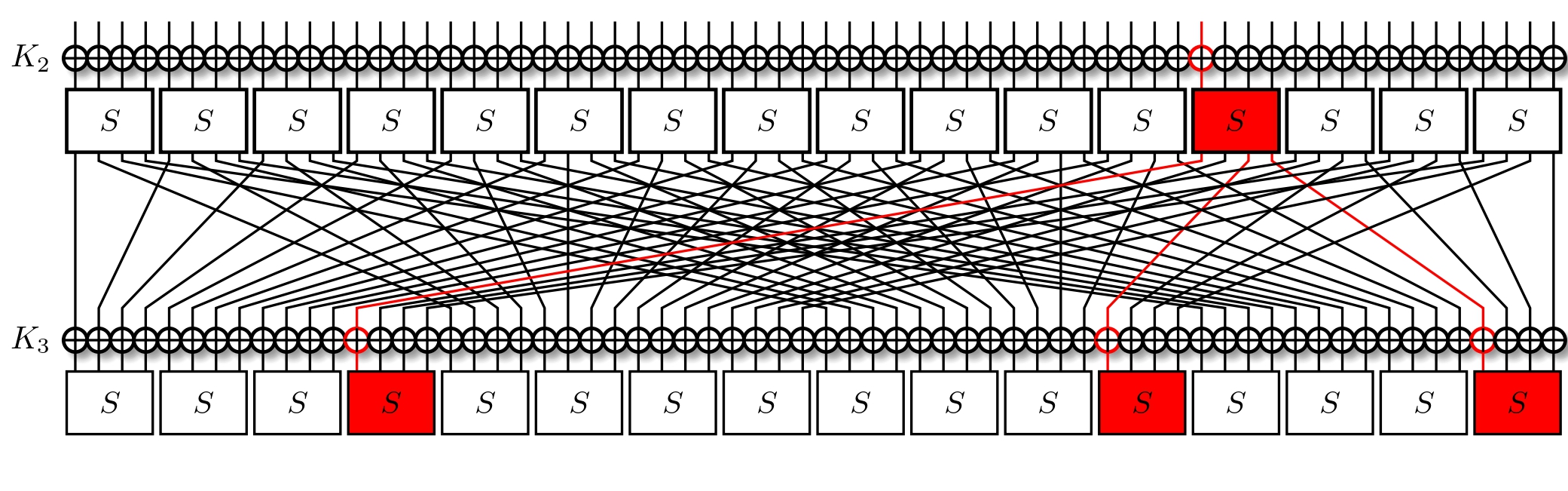
We now have a two-round differential trail that holds with a total probability of $2^{-2} * 2^{-2} = 2^{-4}$. It seems to be going well, but what determines if a trail is good? And what is our goal?

Good differential trails

Active S-Boxes are traditionally something we'd like to minimise as an attacker, and maximise as a designer. The so-called branch number $\mathcal{B}$ for a cipher tells us what the minimal amount of active S-Boxes is for any two consecutive rounds. The lowest it can be is obviously $\mathcal{B} = 2$. Meanwhile, the most it can be for a SPN is $\mathcal{B} = 1 + \text{no. of S-Boxes per round}$ as the first round could only have one S-Box active.

It's not hard to imagine, and in fact is fun to find, the differential trail for PRESENT by which only two S-Boxes would be active in the first two rounds. Finding it is how we may prove that PRESENT has a branch number of two. This can be considered bad in comparison to e.g. AES, which has a branch number of five, but enough rounds can supplant the issue.

Task Find a differential trail which proves that the $\mathcal{B} = 2$ holds for PRESENT. Additionally, find a trail that proves the branch number for three consecutive rounds is $3$.

Theoretical security

Branch numbers are useful as they tell us how many rounds we should aim to have. The PRESENT cipher has a branch number of 2, and a differential uniformity of 4. This means that the minimum amount of active S-Boxes corresponds to the number of rounds, and the maximum probability of a differential per S-Box is $2^{-2}$. This implies that, for its 32 rounds, the best possible differential trail holds with a probability of $({2^{-2}})^{31} = 2^{-62}$. For comparison, a trail wants to hold with a probability better than "random", i.e. the probability of a pair of blocks differing by a desired amount (which is equal to $2^{-64}$ for to the block size of PRESENT).

This above may sound worrying. It is, after all, an argument made that lends belief that PRESENT is weak to differentials. However, in the specification of the cipher, the designers go on to prove that PRESENT's branch number for five consecutive rounds is 10, so for 25 rounds there will be at least 50 active S-Boxes. This is much better than our earlier assumption, and leads to standard differentials trails having a probability of less than $2^{-100}$ over all the rounds.