Hello World!

To keep the course concise, we won't ask you to implement PRESENT from scratch (though you're welcome to do so!) and instead provide you with a finished implementation in TODO.

Traditionally, PRESENT has 32 rounds, with the last round being special. Like most SPNs, each round consists of three important aspects:

• Round key addition: For each round, we XOR the state with the current round key.
• Substitution: The state is subdivided into 4-bit chunks that're put through substitution boxes (S-Boxes). These are bijective maps: four bits go in, four come out.
• Permutation: This is the linear layer of the cipher, responsible for mixing i.e. permuting the bits. It can be expressed as $f(x) = 16 * x \mod 63$, where $x = 0$ is the MSB. The LSB is special, and remains fixed.

A single round is pictured below.

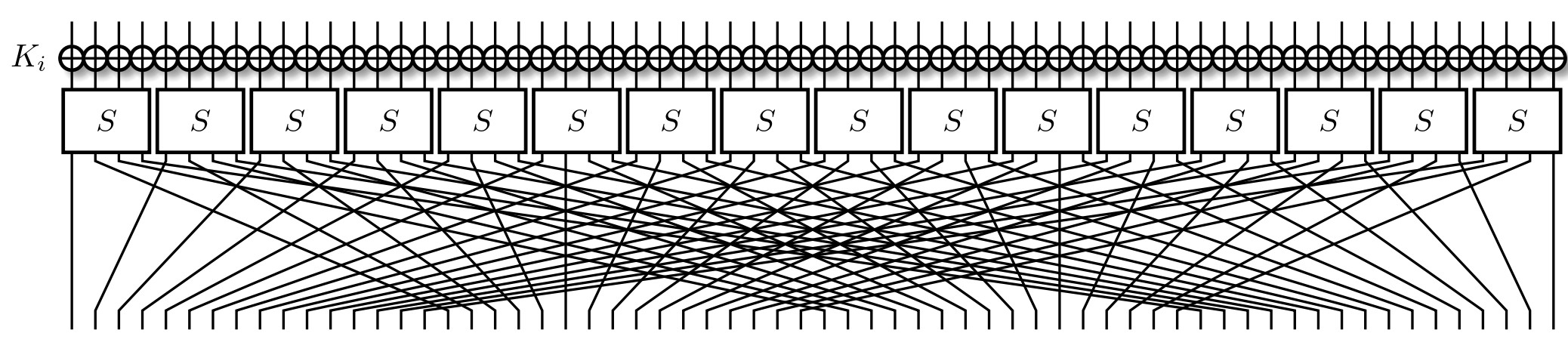
We did mention the last round being special. Unlike the others, it consists of only the round key addition.

Task: The last round of PRESENT does not include substitution and permutation after the key addition. Why?

That are two primary properties a symmetric cipher ought to have: confusion and diffusion. Confusion is the property that each output bit should depend on many input bits. This is a good thing, as the opposite makes the relationship between the ciphertext and key too obvious. This is accomplished via the prior mentioned S-Boxes, as each output bit is (partially) dependent on the four input bits.

The other is diffusion: the property that a slight change in the plaintext ought to influence a lot of the ciphertext, and vice versa. This is desirable because we don't want similar plaintexts to produce similar ciphertexts, and is accomplished via the permutation layer.

With that out of the way, let's try to decrypt a message. Using the key SYMMETRIC_CRYPTO, we've encrypted the following message with regular, 32-round PRESENT. Try to decrypt it, either with the provided implementation, or with your own.

0x823F2D4E3