Meet-in-the-middle

In the previous lesson, we made mention of a key schedule. Most ciphers have one, extending a single key into multiple, round-specific keys. The way PRESENT does this can be found in its specs. What matters right now is that each round has a different round key than any other, and the relationship between any two round keys is largely non-linear.

Obviously, a key schedule of some sort is needed; due to the block size (i.e. the input size) of PRESENT being only 64-bits, a static round key would imply a bit-security of 64 bits too, regardless of how we sample it from the main key. But why do we need different round keys for each and every round?

Suppose we instantiate PRESENT as follows:

def random_roundkey(bits: int):
    t = randint(0, 2**bits)
    return int(sha256(str(t).encode()).hexdigest()[:16], 16)

a, b = random_roundkey(20), random_roundkey(20)

cipher = Present(rounds=32, custom_roundkeys=[a] * 16 + [b] * 16)

Here we have two, 64-bit round keys. One can imagine this to be similar to a key schedule that'd simply split the key in two, and use those as our round keys. In our example, the first sixteen rounds use $K_a$ and the subsequent sixteen use $K_b$ as their round key. However, this proves almost no more secure than having simply used a static round key.

Meet-in-the-Middle

Let’s take a look at a tweaked version of PRESENT that just splits the master key $K$ into two, independent 64-bit round keys: $K_a$ for the first half of the cipher and $K_b$ for the second half.

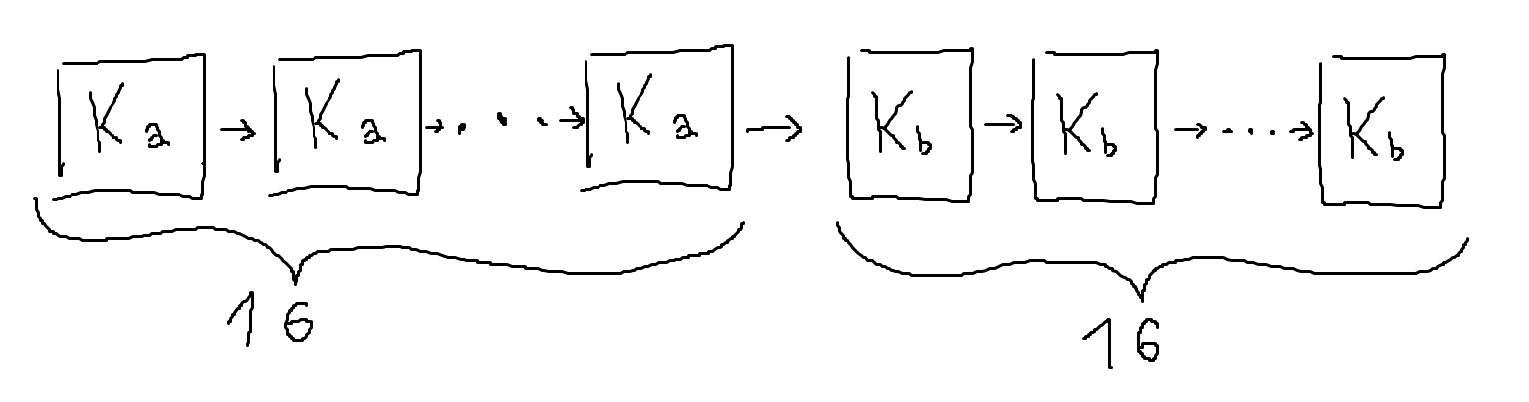
A naive approach would be to brute force both $K_a$ and $K_b$ and decrypt a ciphertext for each pair till the matching plaintext is produced. However, this proves incredibly slow: at two 64-bit round keys, it's a complexity of $2^{64} * 2^{64} = 2^{128}$, way beyond our (or anyone's) capabilities, and is just us guessing the entire key $K$.

Meet-in-the-middle (MITM) attacks are a way to do this more efficiently. The idea is simple: instead of attacking a cipher from one end, we attack it from both, starting from the plaintext side and the ciphertext side, and try to meet someplace in the middle. It’s a clever way to trade memory for speed, which can make brute-force-style attacks such as ours much more practical. The crux of the MITM paradigm is that we don't need to brute force both pairs at once, but that we can do so sequentially instead.

Here's how we'd attack this with a MITM approach:

1. Forward direction (plaintext $\rightarrow$ middle): For each possible value of $K_a$, run the first 16 rounds of the cipher starting from the plaintext $p$. That gives us an intermediate value $m$. We store all $2^{64}$ of these intermediate values in a table.

2. Backward direction (ciphertext $\rightarrow$ middle): Now, for each possible value of $K_b$, we run the last 16 rounds of the cipher in reverse, starting from the ciphertext $c$. For each partial decryption, we get a candidate intermediate value $m'$. Check if it shows up in the table of forward values from step 1.

3. Match found? If a match is found, we’ve probably got a good pair: one key that takes $p$ to $m$, and another that takes $c$ back to that same $m$. This gives us a likely $(K_a, K_b)$ pair.

This brings the time complexity down to about $2^{65}$: one full $2^{64}$ round of forward encryption, one full $2^{64}$ round of backward decryption. Much better than the $2^{128}$ we started with, and goes to show that using two round keys isn't all that great.

Of course, in our case, this comes with a memory trade-off. We have a memory complexity of $2^{64}$ due to storing all the intermediate values

Implement

Let's now write out an attack. Here's our cipher:

def random_roundkey(bits: int):
    t = randint(0, 2**bits)
    return int(sha256(str(t).encode()).hexdigest()[:16], 16)

cipher = Present(rounds=32, custom_roundkeys=[a] * 16 + [b] * 16)

Task Provided the following plaintext / ciphertext pair 059f909aa441d – 3f2341242d412 decrypt the following: 0x432fdffa11